 |
Transformations géométriques Par Xavier Michelon |
 |
Transformations géométriques Par Xavier Michelon |
Il semblerait logique de penser que puisqu'on travaille en 3 dimensions, les matrices utilisées sont elles aussi de dimension 3. En fait ce n'est pas le cas. OpenGL travaille avec des matrices 4x4, dans un système de coordonnées dit "homogène". L'avantage de ce système est qu'il permet de représenter les transformations par des matrices et de composer toutes ces transformations par un simple produit matriciel.
Les points de l'espace sont stockés dans des vecteurs de 4 lignes (voir figure 1). Les 3 premières lignes contiennent respectivement les coordonnées x, y et z du point. La quatrième ligne contient un coefficient noté w, appelé facteur d'échelle, qui vaut souvent 1. Considérons un point P en coordonnées homogènes, pour lequel le facteur d'échelle ne vaut pas 1. Pour retrouver les coordonnées cartésiennes du point, il suffit de diviser toutes les composantes par w. Vous remarquerez qu'avec ce système, un même point de l'espace a une infinité de représentations : les coordonnées (2,10,8,2) et (1,5,4,1) correspondent au même point. Il est également intéressant de noter que les coordonnées homogènes permettent de définir des points situés à l'infini, en choisissant w=0.
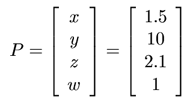 |
| Figure 1 : Représentation d'un point P en coordonnées homogènes |
Vous trouverez sur les figures 2, 3 et 4 les formes des matrices de translation, de rotation, et d'homothétie. Je pense que vous savez ce que sont une rotation et une translation, mais l'homothétie est peut-être plus mystérieuse. Une homothétie est un changement d'échelle de l'objet. Une homothétie uniforme de facteur 2 va faire doubler la taille d'un objet, une homothétie de facteur 0,5 va la diminuer de moitié, et bien sûr, une homothétie de facteur 1 va laisser l'objet à sa taille d'origine. Dans la matrice d'homothétie on trouve 3 facteurs hx,hy et hz. Si ces trois coefficients sont égaux, on est dans le cas d'une homothétie uniforme. Si les facteurs ne sont pas identiques, on a une homothétie non uniforme, qui vous donne la possibilité d'étirer et de rétrécir différemment suivant les axes X, Y et Z.
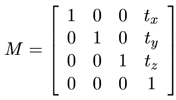 |
| Figure 2 : Matrice de translation de vecteur (tx,ty,tz) |
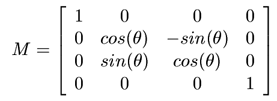 |
| Figure 3 : Matrice de rotation d'angle thêta autour de l'axe x |
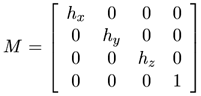 |
| Figure 4 : Matrice d'homothétie de facteurs hx,hy,hz |
Transformer un objet consiste à appliquer la transformation à l'ensemble des points qui le constituent. On souhaite appliquer une transformation de matrice M à un point P. Appelons P' le résultat de la transformation. Le résultat s'obtient par une simple multiplication matricielle P'=M*P. La composition de transformations est toute aussi simple. Supposons qu'on veuille appliquer à une objet une translation de matrice Mt, puis une rotation de matrice Mr. Dans un premier temps, on applique la translation en calculant Mt*P, puis on multiplie à gauche le résultat par Mr. Le résultat de la composition des deux transformations appliquées à P vaut Mr*(Mt*P). Le produit matriciel a pour propriété d'être associatif, ce qui implique que Mr*(Mt*P)= (Mr*Mt)*P. Par conséquent, on peut considérer la composée de transformation comme une unique transformation de matrice Mr*Mt. En revanche, la multiplication matricielle n'est pas commutative, c'est-à-dire que Mr*Mt est à priori différent de Mt*Mr. Ceci implique que l'ordre dans lequel on multiplie les matrices de transformation est crucial, et il est important de noter que puisque nous lisons de gauche à droite, l'ordre d'écriture des matrices est inversé par rapport à l'ordre d'application des transformations.
 |
| Figure 5: Transformation d'un point par composition d'une translation et d'une rotation |
|
|