 Contents
Previous
Next
Contents
Previous
Next
Beginnend mit Version 0.9.92 kann unser Igel die Ebene verlassen und
sich im 3D-Raum bewegen. Wir benutzen das Primitiv perspektivisch
, um dorthin zu schalten. Willkommen in der 3D-Welt!
Die perspektivische Projektion
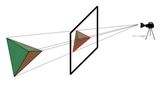
Um einen 3D-Raum in einer 2D-Ebene darzustellen, benutzt XLogo eine perspektivische Projektion. Eine Kamera sieht auf die 3D-Szene und angezeigt wird das Bild des Projektionsschirms. Hier ist ein kleines Schema, das dies erklären soll:
Einige Primitive erlauben die Kameraposition zu setzen, der Projektionsschirm liegt auf halber Entfernung zur Kamera.
 |
|---|
Orientierung in 3D-Welt verstehen
In der Ebene wurde die Orientierung des Igels nur durch seinen Kurs
(kurs) definiert. In der 3D-Welt ist die
Orientierung des Igels durch drei Winkel gegeben:
Rollwinkel: Die Steigung des Igel um die Achse
Oy.
Neigung: Die Steigung des Igel um die Achse Ox.
Kurs: Die Steigung des Igel um die Achse Oz.
Tatsächlich ist der Igel sehr ähnlich zu einem Jet, wenn er sich selbst
in der 3D-Welt bewegt. Hier ist eine kleine Illustration, welche diese
drei Werte darstellt: |  | 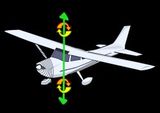 |
|---|
Es erscheint zunächst sehr schwierig zu sein, aber Sie werden sehen, dass die Dinge sehr ähnlich bleiben zu den Bewegungen in der 2D-Ebene. Hier sind die Grund-Primitive für das Bewegen in der 3D-Welt:
vorwärts : Gleiches Verhalten wie in der
2D-Ebene
rechts : Gleiches Verhalten wie in der 2D-Ebene
rollerechts : Der Igel dreht sich um n Grad
rechts um die longitudinale Achse
rollelinks : Der Igel dreht sich um n Grad links
um die longitudinale Achse
rauf : Der Igel geht um n Grad hoch um seine
transversale Achse
runter : Der Igel geht um n Grad hinab um seine
transversale AchseWenn wir in der 2D-Ebene ein 200 Schritte breites Quadrat zeichnen wollen, schreiben wir:
wiederhole 4 [vorwärts 200 rechts 90]
Diese Anweisungen sind auch in der 3D-Welt verfügbar und das Quadrat
wird in dem Modus perspektivisch gezeichnet. Wenn der Igel
90 Grad herunter geht, können wir ein weiteres Quadrat
zeichnen und wir erhalten:
löschebild
wiederhole 4 [vorwärts 200 rechts 90]
runter 90
wiederhole 4 [vorwärts 200 rechts 90]
 |
|---|
Sie müssen gerade einmal ein paar Beispiele probieren, um diese Orientierung zu verstehen und werden ein Experte! Dann werden Sie erkennen, wie die drei Rotations-Primitive verbunden sind. Zum Beispiel versuchen Sie das:
löschebild
rollelinks 90 rauf 90 rollerechts 90
Das Bewegen des Igel ist äquivalent zu links 90.
Verfügbare Primitive im 2D- und 3D-Modus
Die folgenden Primitive sind verfügbar in der Ebene und in der
3D-Welt. Der einzige Unterschied sind die Argumente, die diese
Primitive empfangen. Zum Beispiel warten die Primitive setpos
und setposition immer noch auf ein Listenelement als
Argument. In 3D muss diese Liste aus drei Zahlen bestehen, welche die
drei Punktkoordinaten darstellen. Hier sind diese Primitive:
kreis | bogen | heim
| richtung |
abstand | setzeposition |
setzex | setzey |
setzerichtung | igeltext |
längeigeltext | punkt |
pos | richtung | . | . |
Nur im 3D-Modus verfügbare Primitive
setzexyz : Dieses Primitiv bewegt den Igel zum
gewählten Punkt. Dieses Primitiv wartet auf drei Argumente, die die
Punktkoordinaten darstellen. setzexyz ist sehr ähnlich zu
setzeposition aber die Koordinaten stehen dort nicht als Liste.
Zum Beispiel bewegt setzexyz minus 100 200 50 den Igel zu
dem Punkt x=-100; y=200; z=50setzez : Dieses Primitiv bewegt den Igel zu dem
Punkt mit dem gültigen Wert für z. setzez wartet auf eine
Zahl als Argument. Dieses Primitiv ist vergleichbar zu setzex
und setzey.setzeorientierung : Setzt die Orientierung des
Igel. Dieses Primitiv wartet auf eine Liste, welche drei Zahlen
enthält: den Rollwinkel, die Neigung und die Kurs.
Zum Beispiel setzt setzeorientierung [100 0 58] den
Rollwinkel 100, die Neigung auf 0 und den
Kurs auf 58 Grad.Orientierung : Gibt die Orientierung des Igel in
einer Liste zurück: Rollwinkel , Neigung , Kurs. Beachten
Sie die Zahlenreihenfolge. Zum Beispiel ergibt 100 , 20 , 90
dieselbe Orientierung, wenn nach der Anweisung löschebild
von der Ursprungsposition ausgegangen wird: rollerechts 100 rauf 20 rechts 90
Wenn Sie die Reihenfolge der Anweisungen ändern, erhalten Sie nicht die gültige Orientierung!
setzerollwinkel : Der Igel dreht sich um die
longitudinale Achse und erhält den gewählten Winkel.
rollwinkel : Ergibt den aktuellen Wert des
Rollwinkel.
setzeneigung : Der Igel dreht sich um die
transversale Achse und erhält die gewählte Neigung.
neigung : Ergibt den aktuellen Wert der Neigung.3D Betrachter
Ein 3D-Betrachter ist in XLogo enthalten und erlaubt es Ihre Zeichnungen in 3D darzustellen. Dieses Modul verwendet die Java3D Bibliotheken, so dass es notwendig ist Java3D voll installiert zu haben.
Hier sind die Regeln zur Verwendung des 3D-Betrachters:
Wenn wir geometrische Figuren im Zeichenbereich erschaffen wollen, müssen wir den 3D-Betrachter anweisen, welche Formen wir für zukünftige Darstellungen aufzeichnen wollen. Es ist möglich Vielecke/Vieleckflächen, Linien, Punkte und Text aufzuzeichnen.
Hier sind die Primitive:
vieleckanfang : Die als nächstes folgenden
Igelbewegungen werden gespeichert, um ein Vieleck zu erzeugen.vieleckende : Seit dem letzten Aufruf von
vieleckanfang hat der Igel mehrere Ecken angesteuert. Dieses neue
Vieleck wird aufgezeichnet, seine Farbe wird bestimmt durch alle Farben
der Eckpunkte. Dieses Primitiv vollendet das Vieleck.linienanfang : Die als nächstes folgenden
Igelbewegungen werden gespeichert, um eine Linie zu erzeugen.linienende : Seit dem letzten Aufruf von
linienanfang hat der Igel mehrere Ecken angesteuert. Diese neue
Linie wird aufgezeichnet, seine Farbe wird bestimmt durch alle Farben
der Eckpunkte. Dieses Primitiv vollendet die Linie.punkteanfang : Die als nächstes folgenden
Igelbewegungen werden gespeichert, um eine Punktemenge zu erzeugen.punkteende : Dieses Primitiv beendet die
Punktemenge.textanfang : Jedesmal wenn der Benutzer mit dem
Primitiv igeltext einen Text im Zeichenbereich anzeigt,
wird er aufgezeichnet und dann im 3D-Betrachter angezeigt.textende : Beendet die Texteaufzeichnung.view3d vieleckansicht : Startet den
3D-Betrachter. Alle aufgezeichneten Objekte werden in dem neuen Fenster
gezeichnet. Sie können die Kamera steuern:
Zeichnen eines Würfels
Alle Seitenflächen bestehen aus 400 Schritten breiten Quadraten. Hier ist das Programm:
lerne quadrat
# we record the vertice square
vieleckanfang wiederhole 4[vorwärts 400 rechts 90] vieleckende
Ende
lerne einfacherWürfel
# gelb cube
löschebild perspektivisch setzestiftfarbe gelb
# lateral faces
wiederhole 4[quadrat stifthoch rechts 90 vorwärts 400 links 90 rollerechts 90 stiftab]
# bottom face
runter 90 quadrat rauf 90
# upper face
vorwärts 400 runter 90 quadrat
# visualization
vieleckansicht
Ende
Wir starten das Kommando einfacherWürfel:
 |
|---|
Wenn wir in der Prozedur Quadrat vieleckanfang
durch linienanfang und vieleckende durch
linienende ersetzen:
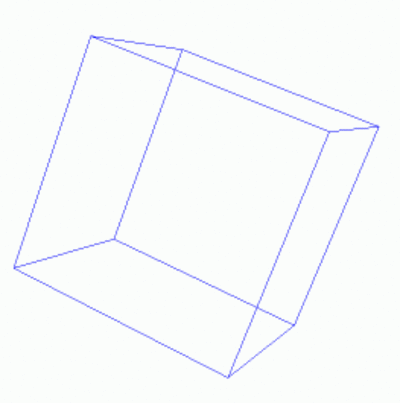 |
|---|
Hätten wir punkteanfang und punkteende
statt linienanfang und linienende verwendet,
sollten wir auf dem Schirm nur die acht Würfelecken sehen. Diese
Primitive sind sehr wichtig zum Darstellen von Punktemengen in 3D.
 Contents
Previous
Next
Contents
Previous
Next