Genius

🗃️ Specifications

📰 Title:	Genius	🕹️ / 🛠️ Type:	Game
🗃️ Genre:	Puzzle	👁️ Visual:	2D & 3D
🏷️ Category:	Puzzle ➤ E-learning ➤ Mathematics	🏝️ Perspective:	Third person
🔖 Tags:	Puzzle; E-learning; Mathematics; Programming; Flagship	⏱️ Pacing:	Real Time
🐣️ Approx. start:		👫️ Played:	Single
🐓️ Latest:	2018-05-15	🚦 Status:	05. Tested & Working (status)
📍️ Version:	Latest: 1.0.24 / Dev: 930e9d5	❤️ Like it:	9. ⏳️
🏛️ License type:		🎀️ Quality:	2. 🏅️⭐⭐⭐⭐ (good)
🏛️ License:		✨️ (temporary):
🐛️ Created:	2018-06-21	🐜️ Updated:	2024-06-22

📦️ Deliverables

📦️ Package name:	gnome-genius, genius	..... 📦️ Arch:
📄️ Source:		..... 📦️ RPM:
⚙️ Generic binary:		..... 📦️ Deb:
🌍️ Browser version:		..... 📦️ AppImage:
📱️ PDA support:		..... 📦️ Flatpak:
✨️ Not use:		..... 📦️ Snap:

🚦 Entry status

📰 What's new?:		👻️ Temporary:
💡 Lights on:		🎨️ Significant improvement:
👔️ Already shown:		💭️ New version published (to be updated):
🎖️ This work:		🚧️ Some work remains to be done:
👫️ Contrib.:	goupildb & Louis	🦺️ Work in progress:
🎰️ ID:	15428

📖️ Summary

📜️[en]:	A libre tool for mathematics, similar to BC, Matlab, Maple or Mathematica. It is used both as a simple calculator and as a research or educational tool. Its interface allows a writing close to mathematics, the programming / design of simulations via its internal language (called GEL), drawing 2D or 3D graphics, export to EPS or PNG format. A lightweight and comprehensive tool that continues to evolve.	📜️[fr]:	Un outil libre pour les mathématiques, similaire à BC, Matlab, Maple ou Mathematica. Il s'utilise à la fois comme une simple calculatrice et comme un outil de recherche ou d'éducation. Son interface permet une écriture proche des mathématiques, la programmation / conception de simulations via son langage interne (dénommé GEL), le tracé de graphiques en 2D ou 3D, l'export au format EPS ou PNG. Un outil léger et complet qui continue d'évoluer.

📕 Description [en]

📜️ "blabla" 📜️

Genius is a general purpose calculator program similar in some aspects to BC, Matlab, Maple or Mathematica. It is useful both as a simple calculator and as a research or educational tool. The syntax is very intuitive and is designed to mimic how mathematics is usually written. GEL is the name of its extension language, it stands for Genius Extension Language, clever isn't it? In fact, many of the standard genius functions are written in GEL itself.

What can it do?

• Arbitrary precision integers, multiple precision floats.
• Rational numbers, stored as quotient and denominator.
• Complex numbers, stored in Cartesian coordinates as usual.
• Math-like-looking expressions, tries to be as much a what-you-mean-is-what-Genius-understands, up to a limit of course.
• Matrix calculations / Linear Algebra, with many related functions.
• Number theory.
• Calculus, numerical and even very limited symbolic calculations.
• Statistics, all the basic statistical functions.
• Numerical equation solving, polynomial roots, etc...
• Combinatorics.
• Most common elementary / trigonometric functions.
• Modular arithmetic, including inversions and modular arithmetic on matrices.
• A complete programming language, with automatic typing. In fact large part of Genius standard library is written in GEL.
• 2D Function line plots, standard 2D graphs of up to 10 functions at once, with possibility to export to EPS or PNG.
• Parametric plots, with possibility to export to EPS or PNG.
• 3D Function surface plots, with possibility to export to EPS or PNG
• Slopefield/Vectorfield plotting.
• GUI IDE where you can edit and run/test your programs.
• Can output matrices in LaTeX, Troff (eqn) or MathML, this is I think a very cool feature that allows you to copy stuff directly from Genius to a document in LaTeX, troff or MathML.

An example expression can look like:
30*70 + 67^3.0 + ln(7) * (88.8/100) + |sin(40)| - 3i

Or perhaps to sum the first 70 terms of the harmonic series one would do:
sum n=1 to 70 do 1/n

To define a function that takes the square of a number and adds one, you could do:
function f(x) = x^2 + 1

To numerically integrate f from -1 to 1:
NumericalIntegral(f, -1, 1)

To factorize a number into primes:
Factorize(123456789)

To solve a linear system Ax=b:
SolveLinearSystem(A,b)

Given y' = x^2 + y, with initial condition y(0) = 0, to find y(1) using Runge-Kutta with 20 increments:
RungeKutta (`(x,y) = x^2 + y, 0, 0, 1, 20)

The original goal of Genius was to build a better BC then BC. That goal has been attained and surpassed long ago with Genius not having much in common with BC anymore. It is now venturing into the territory of Matlab/Octave, Maple and Mathematica, though it is not quite any of these. I do not think it will ever be a replacement for any, but it is already a very good tool for experimentation, and I have used it in research many times.

What does Genius stand for?
I have no idea ... the G could be GNOME or GNU. I think it used to stand for something and I forgot. So now it's just Genius. Originally the window title was "GnomENIUS Calculator" but that just sounded stupid, so that's not it either.

And of course Genius is free software, released under the GNU General Public License.

Future? That is, what will Genius do at some point in the future:

• Better plotting, probably move to PLplot. GtkExtra is has pretty terrible interface, is essentially unmaintained and doesn't look as good as it could. We could also probably just provide direct interface to PLplot allowing genius to do everything PLplot can in addition to some limited high level stuff we do right now.
• Decimal floating point numbers. We should really work in decimal I think.
• Polynomial handling (it does some polynomial handling by using vectors already but it is only for one variable polynomials)
• Some more symbolic calculation (this is connected to polynomial handling). We should be able to at least simplify, if not integrate.
• Handle roots and constants like pi and e symbolically if desired instead of converting to float. We can do both in parallel in fact.
• Better set support (instead of faking it with vectors)

Acknowledgments: During some of the development the author (Lebl) was partially supported by NSF grant DMS 0900885, NSF grant DMS 1362337, University of Illinois at Urbana-Champaign, University of California, San Diego, University of Wisconsin-Madison, Oklahoma State University.

🍥️ Debian:

Advanced general purpose calculator program (GNOME frontend)

Genius is a general purpose calculator program similar in some aspects to BC, Matlab or Maple. It is useful both as a simple calculator and as a research or educational tool. The syntax is very intuitive and is designed to mimic how mathematics is usually written.

This package contains a GNOME frontend for genius.

📕 Description [fr]

Un outil pour les mathématiques, similaire à BC, Matlab, Maple ou Mathematica, par la Genius Team, initié par Jiří Lebl (jirilebl).

Genius est un outil libre pour les mathématiques, similaire à BC (en dépôts), Matlab, Maple ou Mathematica. Il s'utilise à la fois comme une simple calculatrice et comme un outil de recherche ou d'éducation. Son interface permet une écriture proche des mathématiques, la programmation / conception de simulations via son langage interne (dénommé GEL), le tracé de graphiques en 2D ou 3D, l'export au format EPS ou PNG. Un outil léger et complet qui continue d'évoluer.

Genius est un programme de calcul généraliste similaire à BC, Matlab, Maple ou Mathematica. Il est utile à la fois comme une simple calculatrice et comme un outil de recherche ou d'éducation. La syntaxe est très intuitive et est conçue pour imiter la façon dont les mathématiques sont habituellement écrites. GEL est le nom de sa langue d'extension, qui est l'acronyme de Genius Extension Language, intelligent n'est-ce pas ? En fait, beaucoup des fonctions standard de Genius sont écrites en GEL lui-même.

Qu'est-ce que ça peut faire?

• Des entiers de précision arbitraires, des nombres flottants de précision multiples.
• Les nombres rationnels, stockés en tant que quotient et dénominateur.
• Nombres complexes, stockés en coordonnées cartésiennes comme il est d'usage.
• Les expressions ressemblant à des maths, essayent d'être aussi intuitives que "what-you-mean-is-what-Genius-understands" (NdT : le pendant du WYSIWYG, ce que vous voulez dire est ce que Genius comprend), jusqu'à une certaine limite bien sûr.
• Calcul matriciel / Algèbre linéaire, avec de nombreuses fonctions connexes.
• La théorie du nombre.
• Calculs numériques et même, de manière très limitée, des calculs symboliques.
• Statistiques, toutes les fonctions statistiques de base.
• Résolution d'équations numériques, racines polynomiales, etc ...
• Calculs combinatoires.
• Les fonctions élémentaires / trigonométriques les plus courantes.
• L'arithmétique modulaire, incluant les inversions et l'arithmétique modulaire sur les matrices.
• Un langage de programmation complet, avec saisie automatique. En fait, une grande partie de la bibliothèque standard de Genius est écrite en GEL.
• Tracés de lignes de fonction 2D, graphiques 2D standard jusqu'à 10 fonctions à la fois, avec possibilité d'exporter en EPS ou PNG.
• Tracés paramétriques, avec possibilité d'exporter en EPS ou PNG.
• Tracés de surface de fonction 3D, avec possibilité d'exporter vers EPS ou PNG
• Tracé de Slopefield / Vectorfield.
• Une interface (NdT : GUI IDE) où vous pouvez éditer et exécuter / tester vos programmes.
• Peut produire des matrices en LaTeX, Troff (eqn) ou MathML, je pense que c'est une fonctionnalité très cool qui vous permet de copier des choses directement de Genius vers un document en LaTeX, Troff ou MathML.

Un exemple d'expression peut ressembler à:
30*70 + 67^3.0 + ln(7) * (88.8/100) + |sin(40)| - 3i

Ou peut-être pour résumer les 70 premiers termes de la série harmonique nous pourrions faire :
sum n=1 to 70 do 1/n

Pour définir une fonction qui prend le carré d'un nombre et ajoute un, vous pouvez faire:
function f(x) = x^2 + 1

Pour intégrer numériquement f de -1 à 1:
NumericalIntegral(f, -1, 1)

Pour factoriser un nombre en nombres premiers:
Factorize(123456789)

Pour résoudre un système linéaire Ax = b:
SolveLinearSystem(A,b)

Étant donné y '= x ^ 2 + y, avec la condition initiale y (0) = 0, trouver y (1) en utilisant Runge-Kutta avec 20 incréments:
RungeKutta (`(x,y) = x^2 + y, 0, 0, 1, 20)

L'objectif initial de Genius était de construire un meilleur BC que BC. Ce but a été atteint et dépassé il y a longtemps, Genius n'ayant plus beaucoup de points communs avec BC. Il s'aventure maintenant sur le territoire de Matlab / Octave, Maple et Mathematica, bien que ce ne soit pas tout à fait le cas. Je ne pense pas qu'il puisse remplacer aucun des deux, mais c'est déjà un très bon outil d'expérimentation, et je l'ai souvent utilisé en recherche.

À Quoi correspond le terme de Genius ?
Je n'en ai aucune idée ... le G pourrait être GNOME ou GNU. Je pense que cela représentait quelque chose et j'ai oublié. Alors maintenant, c'est juste Genius. A l'origine, le titre de la fenêtre était "GnomENIUS Calculator" mais cela semblait juste stupide, donc ce n'est pas ça non plus.

Et bien sûr, Genius est un logiciel libre, publié sous la licence publique générale GNU.

Le futur ? Autrement dit, de quoi sera doté Genius plus tard ?

• Meilleur tracé, probablement en passant à PLplot (NdT : dans les dépôts Debian). GtkExtra a une interface assez terrible (NdT : à interpréter comme moche), qui est pour l'essentiel non maintenue et ne semble pas aussi bonne qu'elle pourrait l'être. Nous pourrions aussi probablement fournir une interface directe à PLplot permettant à Genius de faire tout ce que PLplot sait faire, plus certaines choses limitées de haut niveau que nous faisons maintenant.
• Les nombres décimaux à virgule flottante. Nous devrions vraiment travailler en décimal, je pense.
• Le traitement polynomial (il effectue déjà du traitement polynomial en utilisant des vecteurs mais seulement pour des polynômes variables)
• Encore du calcul symbolique (connecté à la gestion polynomiale). Nous devrions pouvoir au moins simplifier, à défaut de l'intégrer.
• Manipuler symboliquement les racines et les constantes comme pi et e au lieu de les convertir en nombre flottant. Nous pouvons faire les deux en parallèle en fait.
• Affiner le support (plutôt que de le bidouiller avec des vecteurs)

Remerciements: Pendant une partie du développement, l'auteur (Lebl) a été partiellement soutenu par la subvention NSF DMS 0900885, subvention NSF DMS 1362337, Université de l'Illinois à Urbana-Champaign, Université de Californie, San Diego, Université du Wisconsin-Madison, Oklahoma State University.

🍥️ Debian:

Programme de calcul généraliste et évolué – interface GNOME

Genius est un programme généraliste de calcul similaire dans certains aspects à BC, Matlab ou Maple. Il est utile à la fois en tant que calculatrice simple mais également comme outil de recherche ou éducatif. La syntaxe est très intuitive et pensée pour imiter la façon dont les mathématiques sont habituellement écrites.

Ce paquet fournit le frontal de GNOME pour genius.

🚧️ Installation ➜ 🚀️ Launching [fr]

✔ ⚙️ Installation à partir du binaire

L'interface est en dépôt, il suffit d'installer le paquet.

📄️ Installation à partir du source

• Source non testé.

🚀️ LANCEMENT DE L'INTERFACE:

• Si vous avez installé l'interface à partir d'un paquet : [Alt+F2] puis saisissez : gnome-genius

🕵️ Test [fr]

🕵️ Test (1.0.24 des dépôts Debian) par goupildb :

🎯️ Objectif : Initialisation de l'entrée, tests et premières impressions.

• 🫕️ Installation :
La version des dépôts Debian fonctionne bien.

• 🏗️ Réalisation :

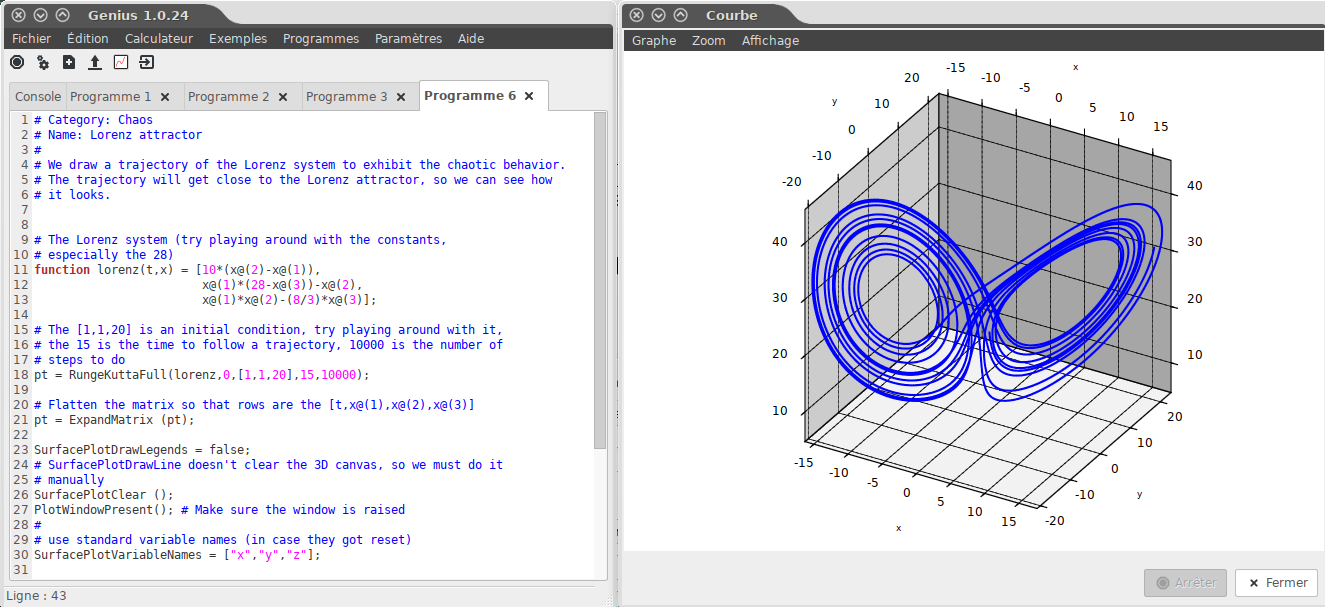
• 🏜️ Graphisme & interface : là non plus je n'ai pas envie de tout passer en revue, juste de vous présenter quelques possibilités. L'interface se présente comme une console (tout Linuxien ne sera donc pas trop dépaysé) avec des onglets

Test de programmes :

Un menu "Exemples" propose des exemples de programmes classés par thèmes.
Il suffit d'en sélectionner un, il s'ouvre dans un onglet, puis de cliquer sur le bouton "Run" (2ème en partant de la gauche), pour voir le programme se lancer dans la console et afficher ses résultats. Si le programme comporte une sortie graphique, une fenêtre de graphique tracera le ou les graphique(s). Certains exemples affichent même une boite de dialogue avec validation.

L'écriture des fonctions mathématiques est intuitive, néanmoins leur mise en oeuvre dans un programme affichant un graphique l'est nettement moins de mon point de vue, car les fonctions graphiques requiert un peu d'apprentissage (dans les 5min je ne suis pas parvenu à tracer un graphique de type y=sin(x) en m'inspirant des exemples :).

Pour tester un graphique de type y=sin(x), il vaut mieux passer directement par le bouton "Tracer" (2ème en partant de la droite), puis dans l'onglet "Tracé de courbes" et sous onglet "Fonction / Expressions" saisir : sin(x) et cliquer sur le bouton "Tracer", c'est immédiat. Notez aussi le résultat obtenu en saisissant y=sin(x) dans l'onglet "Tracé de surface" (l'affichage est en 3D, c'est joli, ça dépasse mes compétences très limitées :).
on peut bien sûr enregistrer son travail et le restituer, faire des exports, et toutes sortes de manips mathématiques, tester des variables, les afficher, etc...

Sinon on peut aussi l'utiliser directement en console en saisissant ses commandes au prompt ("genius>"), du type "4+5", il affiche 9.

L'aide intégrée (malheureusement uniquement en anglais) est assez bien faite :
- le sommaire affiche sous votre navigateur le manuel (en local, pas besoin d'internet)
- l'Aide sur les fonctions affiche celle-ci en tapant les premières lettres ("si" affiche "sin", "sinh", "sign", ...). Chaque fonction mathématique renvoi ensuite vers le site Wikipedia ou Mathworld (et là il faudra donc internet).

• 🐞️ Fiabilité / Robustesse : pas de souci de ce côté là, l'interface fonctionne bien.

‣ 🌞️ J'ai aimé
• Une excellente réalisation (graphisme, interface avec gestion des onglets, aide contextuelle)
• Une interface taillée pour la simulation via des programmes
• De nombreux exemples pré-enregistrés sous l'interface sont fournis
• L'outil est rapide à se lancer, il semble assez véloce (plus que Geogebra qui semble plus lourd et long à se lancer)

‣ 🌤️ Axes d'amélioration
• Elle est un peu moins intuitive et souple que Geogebra, en particulier on ne peux pas intervenir directement sur le graphique
• L'écriture de programmes affichant un graphique n'est pas intuitive (pour tracer une simple fonction du type y=sin(x) il vaudra mieux passer par l'outil de traçage de courbes, mais dans ce cas on perd l'intérêt de la programmation de simulations).

• 🧭️ Conclusion :

🕵️ Impression globale : 👍️
Une calculatrice super évoluée en console et un outil de simulation permettant l'écriture de programmes de mathématiques et le tracé de courbes.
Son point fort semble être (en plus d'être très complet) la légèreté. Son point faible me semble être de nécessiter un certain apprentissage pour le tracé de courbes à partir d'un programme.
Pour le reste c'est parfait, c'est un outil complet et puissant qui ravira les matheux !
👏️ ❤️ Un grand bravo et merci à ses auteurs !