Les tommettes sont des éléments hexagonaux de terre cuite, généralement de couleur feu ou rouge vif, destinés au dallage des sols. Lorsque ces éléments sont carrés, rectangulaires, triangulaires, ou losangés, le pavage plan obtenu est jointif, à savoir qu' à aucun moment la disposition des éléments ne laissera un interstice impossible à combler avec un élément standard. La régularité ordonnée des carreaux est répétitive et prévisible, c'est-à-dire périodique. Cela se vérifie pour tous les carrelages jointifs.
Tous?
Non.
En 1972, Roger Penrose parvint, uniquement par jeu, à réaliser avec des tommettes en
losange, un pavage jointif non périodique (mais presque aurait dit Coluche) à savoir que les mêmes motifs géométriques dessinés se retrouvaient dans le pavage selon une configuration non régulièrement répétitive. Son pavage est qualifié de ce fait de presque périodique, quasi-périodique ou encore : apériodique.
Petites précisions avant d'aller plus loin :
1)- Rien de ce qui vient d'être dit n'est pas vrai pour une forme pentagonale, laquelle ne permet pas le pavage jointif du plan.
2)- Est qualifié de périodique un phénomène qui se reproduit régulièrement identique à lui-même au bout d'une durée appelée : période. Le nombre de fois que se reproduit le phénomène durant l'unité de temps est appelé : fréquence. Mathématiquement, la période est l'inverse de la fréquence, soit P=1/F.
3) - Rappelons qu'un losange est un
parallélogramme dont les quatre côtés sont égaux (un carré sur lequel un individu pondéralement surchargé se serait assis, en somme).
Ce carreleur dilettante, est un mathémathicien doublé d'un physicien, né en 1931 à Colchester, diplômé de la prestigieuse université de Cambridge, professeur au Birkbeck Collège de Londres, où il rencontra le célèbre physicien Stephen W. Hawking avec lequel il travailla sur les origines de l'univers; il apporta sa contribution mathématique à la théorie de la relativité, inventa en 1967 la théorie du twistor liée à l'espace-temps de Minkowski, enseigna à Oxford, s'interrogea en deux ouvrages sur l'Intelligence Artificielle... et trouva le temps d'explorer l'univers des dallages non périodiques, ce qui eut des incidences sur des questions aussi sérieuses que celle de l'existence des mystérieux quasi-cristaux (cristaux quasi-périodiques) découverts en 1984 par les physiciens israéliens Dany Shechtman et Ilan Blecht, l'américain John Cahn et le français Denis Gratias, dont la théorie fut élaborée quelques mois plus tard par les Polytechniciens Michel Duneau et André Katz, lorsqu'ils eurent perçé le secret mathématique qui sous-tend le pavage quasi-périodique.
Petite digression pour prèparer la suite.
On peut se croire un pur esprit rationnaliste -ce qui est une illusion, évidemment-, on ne manquera pas d'être troublé par ce chiffre retors qu'est le chiffre 5.
Ainsi, les milieux cristallins naturels possédent des propriétés de symétrie d'ordre 2, 3, 4 ou 6 (répartition sur 180°, 120°, 90°, 60°), mais jamais d'ordre 5 (72°,2¶/5), ce qui dans le plan correspond à l'angle de répartition des côtés du pentagone, avec lequel il est impossible d'effectuer un pavage jointif. Or le cosinus 72°= 0.30901699437495... peut s'écrire [(((Rac5 + 1)/2)-1)/2], où l'expression ((Rac5 + 1)/2) correspond au fameux (fumeux?)
nombre d'or.
Tiens, qu'est-ce qu'il fait là, lui?
D'ordinaire, lorsqu'on l'évoque, c'est à propos d'harmonie, de beauté de proportions, de joliesse... pas d'impossibilité à créer du beau. Ou alors, il faut admettre que le beau provient justement de cette rupture dans une régularité trop lisse et prévisible, de cette étrangeté qui surgit et surprend agréablement, rompant l'uniformité géométrique.
Mathématiquement, le chiffre 5, non content d'être un nombre premier (divisible uniquement par 1 et par lui-même), se permet d'être un nombre premier de Fermat (1601-1665), un nombre premier de Mersenne (1588-1648), un nombre premier de Wilson, ainsi que le seul et unique nombre premier se terminant par 5, automorphe qui plus est, puisque son carré se termine par le même chiffre que lui-même, ce qui est on ne peut plus normal de sa part étant donné que tous ses multiples se terminent par 5 ou 0. Notons encore qu'il est un terme de la suite de Fibonacci (1170 - 1250), et qu'il est le nombre de millions d'euros qui me pousserait sans réflexion aucune ni le moindre regret vers des vacances définitives. C'est dire sa puissance!
Dans sa graphie européenne, le chiffre 5 est improprement appelé chiffre arabe, comme tous les autres chiffres d'ailleurs, alors qu'ils sont d'origine indienne, brahmanique semble-t'il, hormis lui, ce 5 singulier dont le tracé, aux dires des spécialistes, serait plutôt d'origine khmère et sa forme actuelle véritablement européenne.
Le chiffre 5 se retrouve encore dans le pentagramme, ou étoile à cinq branches (que l'on nomme aussi : pentacle, décagone étoilé), auquel l'imaginaire attribue des vertus fantastiques, soit bénéfiques soit maléfiques selon les charlatans qui l'invoquent. Adopté par les Pythagoriciens, le pentacle était le symbole de l'harmonie; pour les gnostiques, celui des 5 éléments; avec une pointe verticale dirigée vers le bas, il représente la tête de bouc stylisée chère aux satanistes et, pour les franc-maçons, il s'agit de l'étoile flamboyante, c'est-à-dire du soleil qui distribue lumière et vie à la terre et à ses hôtes vivants.
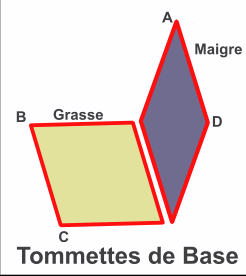
Mais surtout, le chiffre 5 nous intéresse présentement parce qu'il est à la base des tommettes et du pavage de Penrose. Ledit dallage est réalisé à partir de 2 tommettes losangées, de côté évidemment identiques afin de pouvoir les juxtaposer. Les angles des losanges sont égaux à : A=¶/5, B=2¶/5, C=3¶/5, D=4¶/5; le positionnement des losanges, qu'il s'agisse de la tommette maigre ou de la grasse, s'effectue par des rotations multiples de ¶/5 (36°).
Voir illustration : Tommettes de Base.

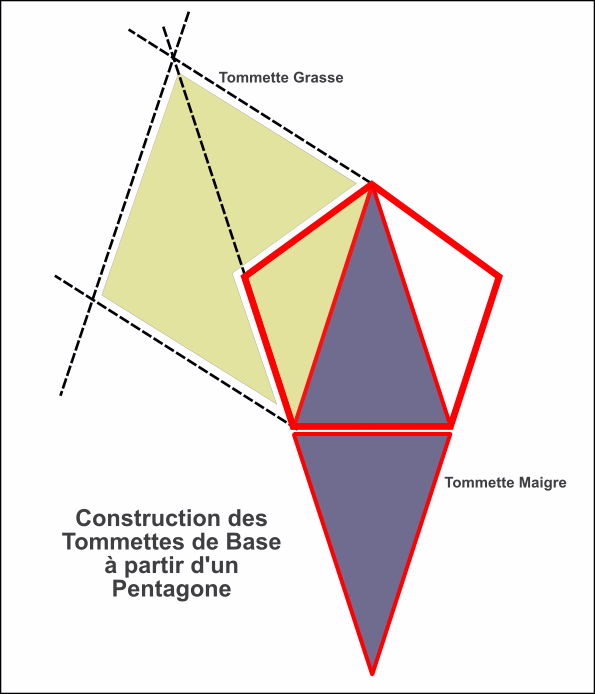
La construction géométrique des tommettes de base peut s'effectuer facilement à partir des 2 triangles isocèles qui résultent de la jonction des sommets du pentagone, triangle que les amateurs d'irrationnels (Il y en a; se reporter à la juteuse industrie des bouquins de Dan Brown ) appellent les triangles d'or, en relation avec le nombre d'or, à cause de l'angle 72° et de son cosinus.
La tommette maigre s'obtient par un copier-coller du triangle bleu auquel on appliquera une symétrie verticale. La tommette grasse nécessite la prolongation de deux côtés du pentagone, du tracé en leur point de concours d'une parallèle à la base du triangle jaune, et enfin du tracé d'une parallèle à ce qui sera un côté du losange.
Sur la figure donnée en exemple, les traits d'esquisse sont laissés en pointillés afin de faciliter la compréhension.
Voir illustration : Construction des Tommettes de base à partir d'un Pentagone.
Oui, mais avec quel programme informatique opérer?
La précision du tracé et du poisitionnement des tommettes imposent l'emploi d'un outil vectoriel, dessin technique (QCad, Varicad...) ou illustration ( Skencil, Inkscape, OpenDraw...). Nous opterons pour ce dernier genre, même si la facilité de dessin rigoureux est moins grande; nous choisirons plus précisément Skencil, à charge pour chacun de transposer le processus dans le programme de son choix. Il s'agit d'une opération extrêmement aisée. De fait, le sujet a également été traité avec Inkscape, et certaines illustrations de ce texte en proviennent.
Donc, Skencil étant ouvert, il convient de préparer le travail.
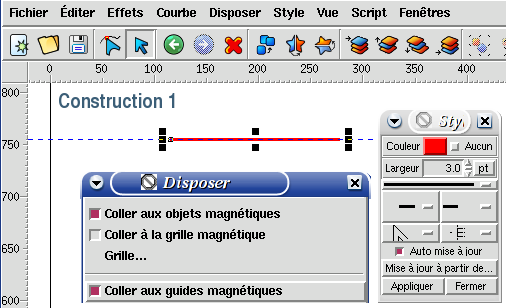
En premier lieu, déposer un guide magnétique horizontal dans l'espace de travail; il servira à tracer un segment parfaitement horizontal, que, d'ailleurs, on aurait pu obtenir en le traçant tout en maintenant la touche Ctrl enfoncée.
Rappelons qu'un guide se dépose de plusieurs manières :
- soit par le menu Disposer> Ajouter une ligne guide horizontale,
- soit en cliquant sur la règle horizontale, et en tirant à la souris le guide qui s'y cache.
Ensuite, activer le magnétisme du guide, et des objets que l'on tracera, pour des raison de précision. Pour cela, dans le menu Disposer, cocher les options Coller aux objets magnétiques et Coller aux guides magnétiques.
Enfin, tracer un segment de longueur quelconque en cliquant sur le guide; le segment résultant est collé au guide : il est donc parfaitement horizontal. Attribuer une couleur et une épaisseur au segment par le menu Fenêtres> Ligne. Pour terminer cette étape, copier le segment ainsi défini dans le presse-papier, par le menu
Editer> Copier, et conserver intact le segment initial qui servira d'étalon en cas de besoin.
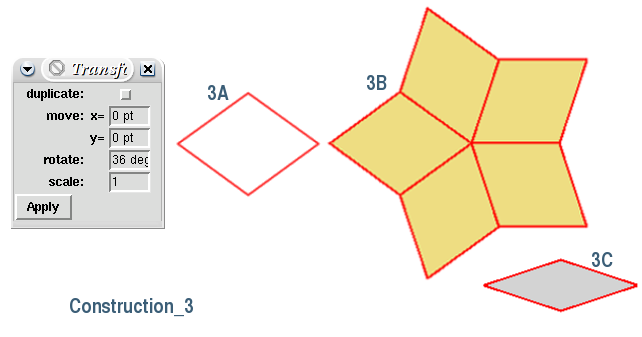
Voir illustration : Construction 1.
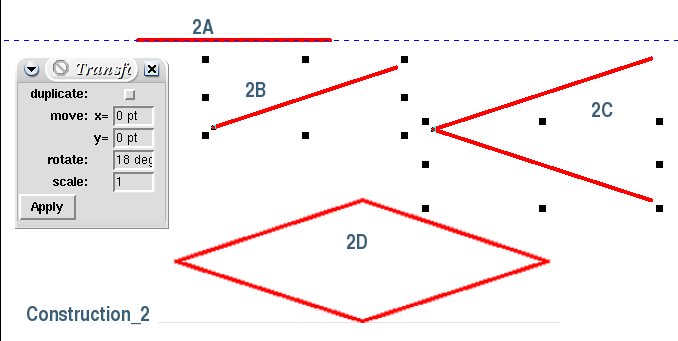
Coller le segment qui se trouve dans le presse-papier; il se place horizontalement (2A).
Le sélectionner s'il ne l'est pas.
Ouvrir la boîte de dialogue Script> Transform, indiquer dans le champ Rotate: 18° et valider par Apply.
Le segment pivote alors (2B).
Coller de nouveau un segment, le faire pivoter de -18 ° puis le joindre au premier pour obtenir une moitié de tommette maigre (2C). Les extrémités des deux segments doivent concourir exactement grâce à la validation de l'option Coller aux objets magnétiques.
Transformer ces deux segments en une polyligne. Pour cela, les sélectionner puis
Courbe> Combiner Bézier.
Les souder en transformant leur point de concours en un noeud commun. Pour cela, la polyligne étant sélectionnée, passer en mode édition de point et désigner le point de concours. Puis activer Courbe> Fermer les noeuds. Sans cette opération, la forme obtenue ne pourra pas être remplie de couleur.
Sélectionner la moitié de tommette, la copier puis la coller.
La symétriser horizontalement par Effets>Retourner horizontalement et enfin la souder à la première moitié de tommette.On dispose alors d'une tommette maigre complète (2C) que l'on remplira à son goût.
Voir illustration : Construction 2.
Il existe des règles rigoureuses pour construire un pavage de Penrose, notamment la méthode dite de N-Grille, dont on trouvera un commentaire ici :
www.membres.lycos.fr/quasicristal/quasi_theme32.html. Il est cependant possible, avec de la patience, du temps devant soi et le goût pour les puzzles de parvenir à un résultat probant, sur une surface certes limitée. Il suffit de savoir à quoi pourrait ressembler la composition finale, bien que celle-ci, avec ses formes imbriquées et ses motifs apparemment mouvants, soit difficile à appréhender. Une petite analyse s'impose donc.
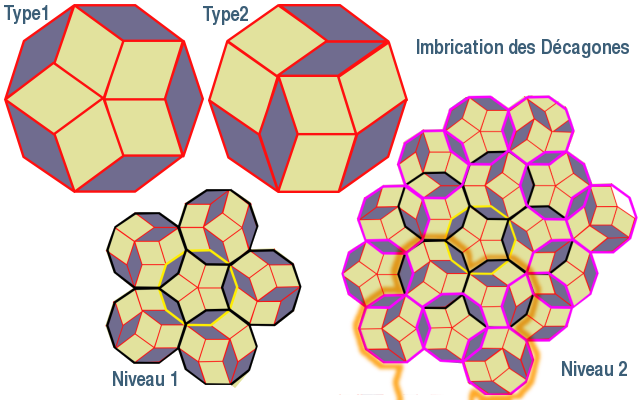
Comme il a déjà été dit, les tommettes s'assemblent par groupe de 5 + 5 formant chacun un décagone. Deux combinaisons sont omniprésentes, voire exclusivement présentes, bien que d'autres dispositions 5 + 5 soient possibles. Il s'agit des pentagones Type 1 et Type 2 sur l'illustration suivante. Le placement des tommettes maigres et grasses les unes par rapport aux se fait grâce à la fonction Script> Transform : Rotate, dans Skencil,
ou Objets> Transformation : Rotation dans Inkscape,
ou encore F4 > Rotation dans StarDraw/OpenDraw
Ces pentagones peuvent être jointifs ou imbriqués, c'est-à-dire que dans ce cas ils se recouvrent partiellement. L'imbrication a lieu sur plusieurs niveaux. Ainsi, si l'on considère un pentagone de Type 1 comme point de départ du pavage (périmètre tracé en jaune sur l'illustration suivante), cinq pentagones de Type2 l'entourent en le recouvrant chacun partiellement mais en étant juxtaposés entre eux (périmètre tracé en noir). Il s'agit d'une imbrication que nous appellerons, par commodités, de Niveau 1.
En agrandissant le champ de vision, on constate que les décagones tracés en noir permettent la composition de nouveaux décagones (périmètre tracé en magenta)s'imbriquant ou se juxtaposant entre eux d'une manière plus complexe. C'est ce que nous avons baptisé l'imbrication de Niveau 2, qui met surtout en évidence que d'autres imbrication de Niveau 1 se forment en partageant partiellement leurs propres décagones (délimitation en orangé).
Voir illustration : Imbrication des décagones.
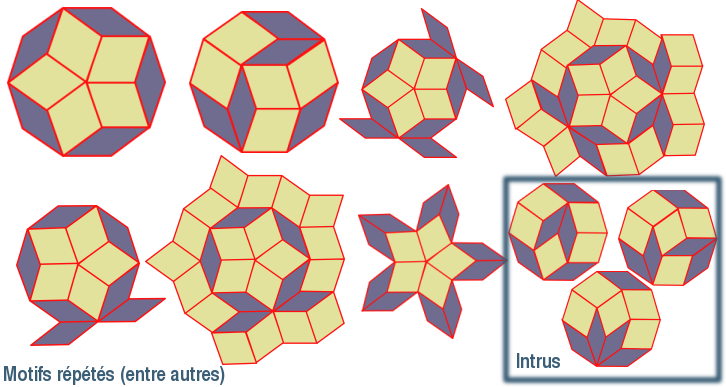
Les imbrications de décagones vont se répéter dans le pavage, créant des grands motifs composés eux-mêmes de motifs plus petits. Nous avons dit que deux types de décagones seraient présents; or il est possible de combiner différemment les tommettes à l'intérieur du décagone, tout en conservant la structure 5 + 5. Ce sont les trois possibilités qui ont été nommés Intrus sur l'illustration suivante. Si nous sommes amenés à les utiliser pour que notre pavage soit jointif, nous qualifierons prudemment celui-ci de quasi-Penrose, voilà tout.
Voir illustration : Motifs répétés.
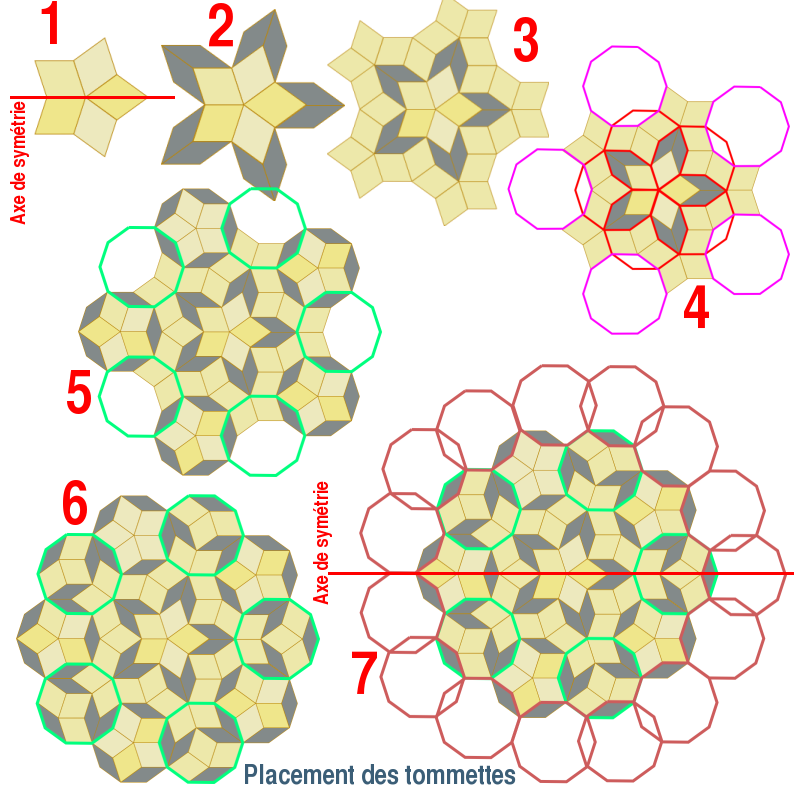
Toute la chronomogie ici décrite est à suivre sur l'illustration "Placement des tommettes". On remarquera que les tommettes grasses ont différentes nuances d'ocre clair : c'est volontaire, l'objectif étant de rompre la monotonie.
Arbitrairement, on décide d'effectuer un pavage circulaire, concentriquement évolutif. Le centre de cette expansion, composé à l'aide de 5 tommettes grasses, est une étoile ayant un axe de symétrie horizontal. En théorie, si le pavage est quasi-périodique, cet axe ne devrait plus pouvoir, à un moment donné, assurer la symétrie (Fig 1).
Les branches de l'étoile sont habillés de tommettes maigres (Fig2), lesquelles sont ceinturées de tommettes grasses comme indiqué par la (Fig3). A ce stade, comment poursuivre? Peut-être suffit-il de constater que nous disposons maintenant d'amorces de cinq décagones rouges et de cinq décagones mauves (Fig4), donc dix en tout, qu'il convient de compléter comme sur la (Fig5), laquelle révèle cinq nouveaux décagones verts à combler. C'est chose faite sur la (Fig6).
Dès cet instant, l'affaire se corse. Car il y a maintenant quinze décagones à compléter (Fig7), et l'on pressent que cela n'ira pas en se simplifiant. Toutefois, le fait d'utiliser un programme informatique nous permet d'abuser du copier-coller, et d'essayer les différentes dispositions admissibles des éléments collés. La boîte de dialogue F4 >Script Transform : Rotate est d'un grand secours pour ce genre de travail.
Voir illustration : Placement des tommettes.
Après des heures de patience étalées sur plusieurs jours, qui ont conduit au 6° ou 7° cercle d'expansion, on peut établir plusieurs constats, à suivre sur l'illustration "Distribution des motifs".
A ce stade, l'axe horizontal d'origine assure toujours la symétrie verticale de l'ouvrage.
Les motifs se répètent suivant les axes des pointes de l'étoile, à savoir tous les 72°, régulièrement distribués sur 360°. Il y a donc 5 motifs répartis sur la totalité de chaque cercle d'expansion, surlignés de différentes couleurs sur l'illustration. D'abord 5 motifs mauves, puis 5 motifs bleus qui s'imbriquent dans 5 motifs rouges; ensuite 5 + 5 motifs verts foncés, puis 5 grands motifs cyans entre lesquels s'intercalent 5 + 5 étoiles qui n'ont pas été surlignées...Toujours des multiples de 5.
Jusque ici, le pavage semble périodique : on peut toujours s'attendre à retrouver un motif à l'endroit où on le cherche. Oui mais : à peine plus loin, voici qu'apparaît un groupement de 3 étoiles en contact les unes avec les autres, groupement qui rompt la distribution par multiples de 5. Il y en a 6 en tout, surlignées en vert clair.
Surprise, surprise!
Etait-ce prévisible? Ai-je commis une erreur ou n'y avait-il pas d'autre solution? Ou s'agit-il du fameux carcatère de non périodicité de ce pavage?
Je laisse aux perspicaces et aux mathématiciens le soin de répondre.
Voir illustration : Distribution des motifs.

Ce petit exercice ne cherche à résoudre aucun mystère géométrique, quel qu'il soit. Il s'agit juste d'utiliser un programme de dessin vectoriel en mettant ses neurones à contribution. Et comme l'on peut vouloir qu'il en résulte quelque chose d'esthétique, nous exportons le travail final en SVG depuis Skencil. Dans Gimp, qui est en mesure de le récupérer, nous le soumettons à un petit effet de relief par >Filtres> Carte> Repoussage d'après une carte, puis, pour en modifier la teinte d'une façon non uniforme, nous activons
>Filtres> Rendu> Brushed metal appliqué sur un nouveau calque, et enfin nous mélangeons celui-ci avec le calque d'origine en mode Teinte. Le reste, tout le monde sait le faire.
Voir illustration : Au final, après passage dans Gimp.
